Quantum Vortex 3D Pattern using Python

 

import matplotlib.pyplot as plt

import numpy as np

from mpl_toolkits.mplot3d import Axes3D

theta=np.linspace(0,20*np.pi,1000)

z=np.linspace(-2,2,1000)

r=z**2+1

x=r*np.sin(theta)

y=r*np.cos(theta)

fig=plt.figure(figsize=(6,8))

ax=fig.add_subplot(111,projection='3d')

ax.plot(x,y,z,color='cyan',linewidth=2)

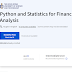
ax.set_title('Quantum Vortex Pattern',fontsize=18,color='purple')

ax.set_facecolor('black')

fig.patch.set_facecolor('black')

ax.grid(False)

ax.set_xticks([])

ax.set_yticks([])

ax.set_zticks([])

plt.show()

#source code --> clcoding.com 

Code Explanation:

1. Import Required Libraries

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

Purpose:

numpy → For mathematical calculations like arrays, linspace, trigonometric functions.

 matplotlib.pyplot → For plotting the graph.

 mpl_toolkits.mplot3d → To enable 3D plotting using Matplotlib.

 2. Define the Vortex Parameters

theta = np.linspace(0, 20 * np.pi, 1000) 

z = np.linspace(-2, 2, 1000)            

r = z**2 + 1

Explanation:

theta → Controls the angle of the spiral (0 to 20π means multiple spiral loops).

 z → Controls the vertical height of the plot (-2 to 2 units).

 r → Radius of the spiral at each z height.

(As z increases or decreases, radius changes — gives a vortex or tornado effect).

 3. Generate X, Y, Z Coordinates

x = r * np.sin(theta)

y = r * np.cos(theta)

Purpose:

Parametric equations of a spiral in 3D:

 x depends on sin(theta)

 y depends on cos(theta)

 z is already defined.

 This gives the 3D twisted spiral shape.

 4. Create 3D Plot Figure

fig = plt.figure(figsize=(10, 7))

ax = fig.add_subplot(111, projection='3d')

Explanation:

Create a new figure of size 10x7.

 Add a 3D subplot to draw 3D patterns.

 5. Plot the Quantum Vortex

ax.plot(x, y, z, color='cyan', linewidth=2)

Purpose:

Draw the 3D vortex spiral using the x, y, z points.

 Color: Cyan

 Line width: 2

 6. Styling the Plot

ax.set_title('Quantum Vortex 3D Pattern', fontsize=18, color='purple')

ax.set_facecolor('black')

fig.patch.set_facecolor('black')

ax.grid(False)

Purpose:

Add a custom title to the plot.

 Set background color of the plot & figure to black for a "space" or "quantum" look.

 Disable grid lines for a clean visual.

 7. Remove Axis Ticks

ax.set_xticks([])

ax.set_yticks([])

ax.set_zticks([])

Purpose:

Remove the axis ticks (numbers) for an aesthetic and clean design.

 8. Show the Final Plot

plt.show()

Purpose:

Display the final 3D vortex pattern on the screen.